Chapter 3 Discounted cost MDPs
In this chapter, we study the discounted MDP model, and derive results/algorithms that parallel the development in SSPs. The goal here is to find the optimal discounted cost \(J^*(i)\) , i.e: \[\begin{align} J^*(i) &= \min_{\pi \in \Pi} J_\pi(i), \forall i, \textrm{ where}\\ J_\pi(i) &= \mathbb{E}\left[ \sum_{k=0}^{\infty} \alpha^k g(x_k, \pi(x_k), x_{k+1}) | x_0 = i \right]. \end{align}\] In the above, \(0 < \alpha < 1\) is a discount factor, \(g(x_k, \pi(x_k), x_{k+1})\) is the single stage cost, \(\pi(x_k)\) is the policy, and \(x_0\) is the start state.
Let \(\pi^*\) denote the optimal policy i.e, \[\pi^* = \mathop{\textrm{argmin}}_{\pi \in \Pi} J_\pi(i)\] and let \(\mathcal{X}= \{1,\ldots,n\}\) denote the state space.
For the analysis, we make the following assumption:
(A1) We shall assume that the single stage cost is bounded, i.e \(|g(.,.,.)| \leq M < \infty.\)
Note that, unlike SSPs, we do not assume the existence of a special termination state.
3.1 Bellman and another operator
For \(J = (J(1), \ldots T(n) )\), we define the Bellman operator \(T\) as follows: \[\begin{align} (TJ)(i) = \min_{a\in A(i)} \sum_{j=1}^n p_{ij}(a)\left(g(i,a,j)+\alpha J(j) \right), \forall i. \end{align}\]
For a stationary policy \(\pi\), we define the operator \(T_\pi\) as follows: \[\begin{align} (T_\pi J)(i) = \sum_{j=1}^n p_{ij}(\pi(i))\left(g(i,\pi(i),j)+\alpha J(j) \right), \forall i. \end{align}\]
To simplify notation, we shall write the \(T_\pi\) operator in vector-matrix notation. For this purpose, we define the quantities \(P_{\pi}\) and \(g_{\pi}\), denoting the transition probability matrix and single stage cost vector underlying a given policy \(\pi\). Let \[P_{\pi}=\begin{bmatrix} p_{11}(\pi(1)) & p_{12}(\pi(1)) & p_{13}(\pi(1)) & \dots & p_{1n}(\pi(1)) \\ p_{21}(\pi(2)) & p_{22}(\pi(2)) & p_{23}(\pi(2)) & \dots & p_{2n}(\pi(2)) \\ \vdots & \vdots & \vdots & \ddots & \vdots \\ p_{n1}(\pi(n)) & p_{n2}(\pi(n)) & p_{n3}(\pi(n)) & \dots & p_{nn}(\pi(n)) \end{bmatrix},\] and \[g_{\pi}=\begin{bmatrix} \sum_{j = 1}^n p_{1j}(\pi(1)) g(1,\pi(1),j)\\ \sum_{j = 1}^n p_{2j}(\pi(2)) g(2,\pi(2),j)\\ \vdots\\ \sum_{j = 1}^n p_{nj}(\pi(n)) g(n,\pi(n),j)\\ \end{bmatrix}\]
If the single stage cost is a function of the current state and current action only, i.e, \(g(i,a,j) = g(i,a) \forall j\), then we can write \(g_{\pi}\) as \[g_{\pi}=\begin{bmatrix} g(1,\pi(1))\\ g(2,\pi(2))\\ \vdots\\ g(n,\pi(n))\\ \end{bmatrix}\] Using vector-matrix notation, it is easy to see that \[T_\pi J = g_\pi + \alpha P_\pi J.\] We will establish below that the operators \(T\) and \(T_\pi\) are monotone.
Lemma 3.1 (Monotone Bellman operator) Let \(J,J' \in \mathbb{R}^n\) and satisfies
\(J(i) \le J'(i), \forall i\).
Then, for any \(k=1,2,\ldots,\) and for any stationary policy \(\pi\), we
have
\((T^kJ)(i) \le (T^kJ')(i)\); and
\((T_\pi^kJ)(i) \le (T_\pi^kJ')(i)\).
Proof. The proof for this is very similar to the proof of Lemma 2.1, i.e., we can use the same arguments here, and prove by induction. The detailed proof is omitted.
A variant of the constant shift lemma, shown earlier in the SSP case, holds here as well. We state this result below.
Lemma 2.2 (Constant shift lemma) Let \(\pi\) be a stationary policy, \(e\) be a vector of ones and \(\delta\) a positive scalar. Then, for \(i=1,\ldots,n\), \(k=1,2,\ldots,\) we have
\((T^k(J+\delta e))(i) \le (T^kJ)(i) + \alpha^k\delta\); and
\((T_\pi^k(J+\delta e))(i) \le (T_\pi^kJ)(i) + \alpha^k\delta\).
Further, the inequalities above are reversed for \(\delta < 0\).
Proof. The complete proof is left as an exercise to the reader, as the arguments used in the corresponding SSP claim can be used to prove this lemma.
3.2 Equivalence of discounted MDP and SSP
Given a discounted MDP on states \(\{1,\ldots,n\}\). we can always reformulate it as an SSP on states \(\{1,\ldots,n\} U \{T\}\), we add the extra state \(T\) which is cost-free and absorbing.
Idea : In the SSP, with probability \(\alpha\), we pick a next state according to transition probabilities of the discounted MDP or with probability \(1-\alpha\), we move to \(T\).
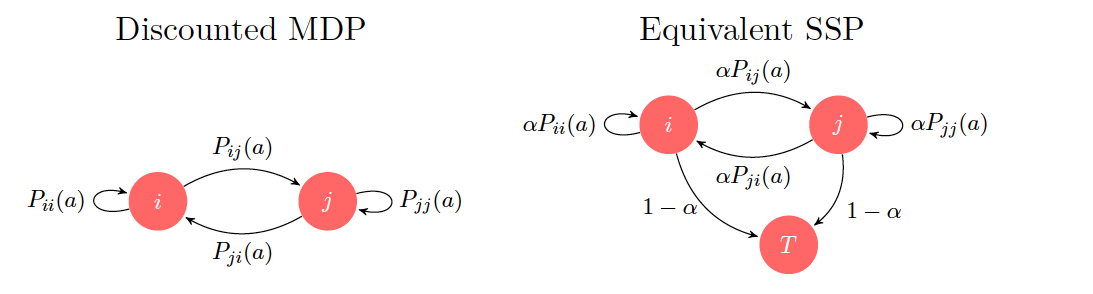
Figure 3.1: Two equivalent problems
Why are these two MDPs equivalent?
Note that in the SSP, all the policies are proper.
In the discounted MDP, the expected \(k^{th}\) stage cost is \[\begin{align} \mathbb{E}\left( \alpha^k g(i, a, j) \right) = \alpha^k \sum_{j} p_{ij}(a) g(i,a,j) \end{align}\]
In the SSP, expected \(k^{th}\) stage cost is \[\begin{align} \left[ \sum_{j} p_{ij}(a) g(i,a,j) \right] \alpha^k \end{align}\] If the terminal cost is not hit upto the \(k^{th}\) stage, then the underlying probabilities will have a \(\alpha^k\) multiplier.
3.3 Bellman equation and fixed point theory
We first state and prove a result that shows repeated application of the Bellman operator leads to the optimal discounted cost. This result forms the basis for value iteration algorithm presented later. ::: {.proposition #discmdp1} For any finite \(J\) and \(\forall i\), the optimal cost satisfies \[J^{*}(i) = \lim_{N \to \infty} (T^NJ)(i).\]
In addition, for a stationary policy \(\pi\), any given \(J\) and \(\forall i\), we have \[J_{\pi}(i) = \lim_{N \to \infty} (T^N_{\pi}J)(i).\] :::
Proof. Given a policy \(\pi = \{\mu_0, \mu_1, ...\}\), and a state \(i \in \chi\), \[\begin{align} J_{\pi}(i) &= \lim_{N \to \infty} \mathop{\mathbb{E}}\left(\sum_{l = 0}^{N-1} \alpha^lg(x_l, \mu_l(x_l), x_{l+1})\right)\\ & = \mathop{\mathbb{E}}\left(\sum_{l = 0}^{L-1} \alpha^lg(x_l, \mu_l(x_l), x_{l+1})\right) + \lim_{N \to \infty} \mathop{\mathbb{E}}\left(\sum_{l = L}^{N-1} \alpha^lg(x_l, \mu_l(x_l), x_{l+1})\right). \end{align}\] Rearranging and adding \(\alpha^LJ(x_L)\) to both sides we get \[\begin{align} \mathop{\mathbb{E}}\left(\alpha^LJ(x_L)+\sum_{l = 0}^{L-1} \alpha^lg(x_l, \mu_l(x_l), x_{l+1})\right) =\\ J_{\pi}(i)-\lim_{N \to \infty} \mathop{\mathbb{E}}\left(\sum_{l = L}^{N-1} \alpha^lg(x_l, \mu_l(x_l), x_{l+1})\right)+\alpha^LJ(x_L).\tag{3.1} \end{align}\] Since \(|g(., ., .)| \leq M\) by assumption, we have \[\lim_{N \to \infty} \mathop{\mathbb{E}}\left(\sum_{l = L}^{N-1} \alpha^lg(x_l, \mu_l(x_l), x_{l+1})\right) \leq M \sum_{l = L}^{\infty}\alpha^l = \frac{M\alpha^L}{1-\alpha}.\] Using the bound above in (3.1), we obtain \[\begin{align} &J_{\pi}(i)-\frac{M\alpha^L}{1-\alpha}-\alpha^L\max_{j \in \chi}|J(j)|\\ \leq \mathop{\mathbb{E}}\left(\alpha^LJ(x_L)+\sum_{l = 0}^{L-1} \alpha^lg(x_l, \mu_l(x_l), x_{l+1})\right) \leq\\ &J_{\pi}(i)+\frac{M\alpha^L}{1-\alpha}+\alpha^L\max_{j \in \chi}|J(j)| \end{align}\] Taking the infimum over \(\pi\) in the inequalities above, we obtain \(\forall i \in \chi\) and any \(L > 0\), \[\begin{align} &J^*(i)-\frac{M\alpha^L}{1-\alpha}-\alpha^L\max_{j \in \chi}|J(j)|\\ & \leq (T^LJ)(i) \leq J^*(i)+\frac{M\alpha^L}{1-\alpha}+\alpha^L\max_{j \in \chi}|J(j)| \end{align}\] In the above, we used the fact that \(\min_{\pi} T^L_{\pi} = T^L\) Now, taking \(\lim_{L \to \infty}\) on all sides, we obtain \[J^*(i) \leq \lim_{L \to \infty} (T^LJ)(i) \leq J^*(i)\] In the above, we used the fact that \(\alpha \in (0, 1)\). The main claim follows.
The second claim follows by considering an MDP where the only feasible action in a state \(i\) is \(\pi(i)\), \(\forall i\), and invoking the first claim in the proposition statement. Note that \(T = T_{\pi}\) for this MDP.
Proposition 3.1 The optimal discounted cost \(J^{*}\) satisfies \[J^{*}=TJ^{*}\] or \[J^{*}(i)=\min_{a \in \mathcal{A}(i)} \sum_{j} p_{ij}(a) (g(i,a,j)+\alpha J^{*}(j))\] Also, \(J^{*}\) is the unique fixed point of \(T\).
Proof. From the proof of the proposition 1, we have \[J^{*}(i) - \frac{M\alpha ^{L}}{1-\alpha} - \alpha ^{L} \max_{j \in \mathcal{X}}|J(j)| \le (T^{L}J)(i) \le J^{*}(i) + \frac{M\alpha ^{L}}{1-\alpha} + \alpha ^{L} \max_{j \in \mathcal{X}}|J(j)|.\] Now, applying \(T\) and using constant shift lemma, we obtain \[TJ^{*}(i) - \frac{M\alpha ^{L+1}}{1-\alpha} - \alpha ^{L+1} \max_{j \in \mathcal{X}}|J(j)| \le (T^{L+1}J)(i) \le TJ^{*}(i) + \frac{M\alpha ^{L+1}}{1-\alpha} + \alpha ^{L+1} \max_{j \in \mathcal{X}}|J(j)|.\] Taking \(L \rightarrow \infty\), we obtain \[TJ^{*}(i) - 0 - 0 \le J^{*}(i) \le TJ^{*}(i) + 0 + 0.\] \[\implies TJ^{*}(i) = J^{*}(i)\] This shows that \(J^{*}\) satisfies the the Bellman equation \(J^{*}=TJ^{*}\).
To establish uniqueness, let \(J'\) be a different fixed point of \(T\). We have \[\lim_{L \to \infty} J' = TJ' = T^{2}J'=...= T^{L}J'\] However, \[\lim_{L \to \infty} T^{L}J' = J^{*} \implies J'=J^{*}.\] Thus, \(J^{*}\) is the unique fixed point of \(T\).
For the corollary, the same approach follows by replacing \(T\) with \(T_{\pi}\) and \(J^{*}\) with \(J_{\pi}\) for both satisfying the Bellman equation and uniqueness.
Corollary 3.1 For a stationary policy \(\pi\), it satisfies \[J_{\pi}=T_{\pi}J_{\pi}\] or \[J_{\pi}(i)=\sum_{j} p_{ij}(\pi (i)) (g(i,\pi (i),j)+\alpha J_{\pi}(j))\] Also, \(J_{\pi}\) is the unique fixed point of \(T_{\pi}\).*
(#prp:prop_n_s) Let \(\mathcal{X}\) denotes the state-space of the infinite horizon MDP setting. A stationary policy \(\pi\) is optimal if and only if \(\pi(i)\) attains the minimum in the Bellman equation, \(\forall i \in \mathcal{X}\) or, equivalently we have \[TJ^{*} = T_{\pi}J^{*}\]
The above proposition defined in Proposition 3 indicates the necessary and sufficient condition for an optimal policy and the proof of the proposition goes as follows.
Proof. Assume \(TJ^{*} = T_{\pi}J^{*}\). We need to show that \(\pi\) is optimal. Using \(J^{*} = TJ^{*}\), we obtain \[\begin{align} J^{*} = TJ^{*}= T_{\pi}J^{*}= J_{\pi}. \end{align}\] Thus, \(\pi\) is optimal.
To prove the converse, suppose \(\pi\) is optimal. Then, \[\begin{align} J^{*} = J_{\pi} = T_{\pi}J^{*}. \end{align}\] From the Bellman equation \(J^{*} = TJ^{*}\) and the equation above, we have \(T_{\pi}J^{*} = TJ^{*}\).
3.4 Contraction property of \(T\) and \(T_\pi\)
Definition 3.1 (Max-norm): The max-norm of a vector is defined as \[||J||_{\infty} = \max_{i=1,\ldots,n} |J(i)|\]
We next show that \(T,T_{\pi}\) are \(\alpha-\)contractions in \(||.||_{\infty}\).
(#prp:prop_n2) For any two bounded \(J, J'\) and \(\forall k \geq 1\), we have \[||T^kJ - T^kJ'||_{\infty} \leq \alpha^k ||J-J'||_{\infty}\]
Proof. Let \(C = \max_{i=1,2,\ldots,n} |J(i) - J'(i)|\)
Hence, \(J(i) - C \leq J'(i) \leq J(i) + C\)
Apply \(T^k\) on all sides of the above inequality expression and use
constant shift lemma to obtain
\[(T^kJ)(i) - \alpha^k C \leq (T^kJ')(i) \leq (T^kJ)(i) + \alpha^k C\]
\[\implies |(T^kJ)(i) - (T^kJ')(i)| \leq \alpha^k C, \forall i\] Taking
max over \(i\) proves the proposition.
Corollary 3.2 For any stationary \(\pi\) and bounded \(J,J'\) and \(\forall k \geq 1\), \[||T_{\pi}^k J - T_{\pi}^k J'||_{\infty} \leq \alpha^k ||J-J'||_{\infty}\]
Note: For value iteration, we start with \(J_0\) and repeatedly apply
\(T\). Hence, the error bound for value iteration would be
\[||T^kJ_{0} - J^{*}||_{\infty} \leq \alpha^k ||J_{0} - J^*||_{\infty}\]
We can get this by setting \(J^{'} = J^{*}\) in
proposition 4 and
taking \(T^{k}J^{*} = J^{*}\).
3.5 Machine replacement example
Consider the infinite horizon discounted version of the machine replacement problem introduced in Chapter 1. In this problem, we want to operate efficiently a machine that can be in any of the \(n\) states, denoted \(1,2,\ldots,n\). State 1 corresponds to a machine in perfect condition. The transitions probabilities \(P_{ij}\) are assumed to be known in prior. \(g(i)\) denotes the cost incurred by the machine in one time period for operating in state \(i\). The actions in each of the states could be
Let the machine operate for one more period in the state it currently is (or)
Replace the machine with a new machine (state \(1\)) at cost \(R\).
If the action in state \(i\) is chosen as to replace the machine i.e., if the machine is replaced once, the machine is guaranteed to stay in state 1 for one period; in subsequent periods, it may deteriorate to state \(j \geq 1\) according to the transition probabilities \(p_{1j}\). To this problem setting introduced earlier, we now consider an infinite horizon and a discount factor \(\alpha \in (0,1)\), so the theory behind applies. Writing down the Bellman equations for the problem setting, we have \[J^{*}(i) = \min\{R + g(1) + \alpha J^{*}(1), g(i) + \alpha \sum_{j=1}^n p_{ij}J^{*}(j)\}\] The optimal action is to repair if it satisfies \[R + g(1) + \alpha J^{*}(1) \leq g(i) + \alpha \sum_{j=1}^n p_{ij}J^{*}(j)\] and we do not repair if \[R + g(1) + \alpha J^{*}(1) > g(i) + \alpha \sum_{j=1}^n p_{ij}J^{*}(j)\] In case of do nothing or do not repair case, consider the following two assumptions. Assume
\(p_{ij} = 0\) if \(j < i\), which implies that machine cannot get any better if you do nothing.
\(p_{ij} \leq p_{(i+1)j}\) if \(i < j\), which implies that it is more likely to jump to a worse state from a state which is closer to it than a state which is farther away.
Suppose, \(J\) is monotone non-decreasing i.e., \(J(1) \leq J(2) \leq \ldots \leq J(n)\), then \[\sum_{j=1}^n p_{ij} J(j) \leq \sum_{j=1}^n p_{(i+1)j}J(j), \forall i \in \{1,2,\ldots,n-1\}.\] Since \(g(i)\) is non-decreasing, we have \((TJ)(i)\) non-decreasing in \(i\), if \(J\) is non-decreasing. Implies, \((T^kJ)(i)\) is non-decreasing in \(i\), \(\forall k\). Hence, \(J^{*}(i) = \lim_{k \to \infty} (T^k J)(i)\) is non-decreasing in \(i\) which in turn implies that the function \(g(i) + \alpha \sum_{j} p_{ij} J^{*}(j)\) is non-decreasing in \(i\). Let \(S_R\) denotes the set of states where it is optimal to repair i.e., \[S_R = \{i | R + g(1) + \alpha J^{*}(1) \leq g(i) + \alpha \sum_j p_{ij} J^{*}(j)\}\] and let \(i^{*}\) be the smallest state in \(S_R\) if \(S_R\) is not empty and \(n+1\) otherwise.
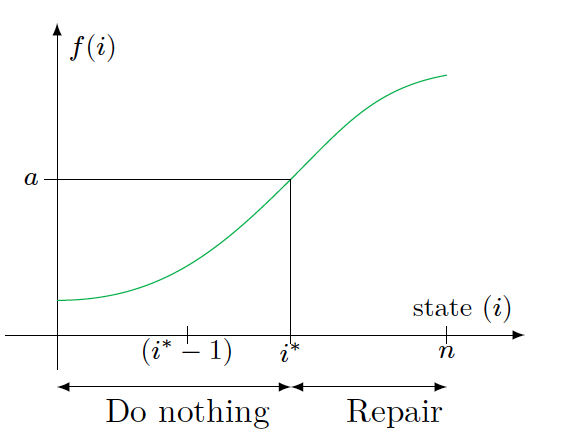
Figure 3.2: The threshold policy for machine replacement problem
Then, the optimal policy would be to replace or repair if and only if \(i \geq i^{*}\). This leads to a threshold based optimal policy as depicted in Figure 3.2, where \(a = R + g(1) + \alpha J^{*}(1)\) and \(f(i) = g(i) + \alpha \sum_{j=1}^n p_{ij}J^{*}(j)\).
Exercise 3.1 Think about policy iteration for this problem. In
particular, if we start with a threshold-based policy and do policy
improvement, then does it lead to another threshold-based policy? If
yes, then policy iteration converges to optimal policy in at most \(n\)
iterations.
3.6 Illustrative example for value iteration
Given the MDP: \[S = \{1,2\}, A = \{ a,b \}\] \[P(a) = \begin{bmatrix}
P_{11}(a) & P_{12}(a)\\
P_{21}(a) & P_{22}(a)
\end{bmatrix} = \begin{bmatrix}
3/4 & 1/4\\
3/4 & 1/4
\end{bmatrix}\] \[P(b) = \begin{bmatrix}
P_{11}(b) & P_{12}(b)\\
P_{21}(b) & P_{22}(b)
\end{bmatrix} = \begin{bmatrix}
1/4 & 3/4\\
1/4 & 3/4
\end{bmatrix}\] Costs:
\(g(1,a) = 2, g(1,b) = 0.5, g(2,a) = 1, g(2,b) = 3\)
Discount: \(\alpha = 0.9\)
\(J_0 = (0,0)\)
\((TJ)(i) = min\{g(i,a)+\alpha \sum_{j=1}^{2} P_{ij}(a)J(j),g(i,b)+\alpha \sum_{j=1}^{2} P_{ij}(b)J(j)\}\)
\(J_1 = TJ_0 = (0.5,1),J_2 = (1.28,1.56)\) and so on.
3.7 Policy iteration
Step 1 : Start with a policy \(\pi_0\)
Step 2 (Policy Evaluation) : Evaluate \(\pi_k\) , i.e., compute
\(J_{\pi_k}\) by solving \(J = T_{\pi_{k}}J\)
\[\label{eq_*}
\iff J(i) = \sum_j P_{ij}(\pi_{k}(i)) (g(i,\pi_{k}(i),j)) + \alpha J(j)),\forall i\]
(Here, \(J(1),...J(n)\) are the unknowns and solving
equation @ref(#eq_*)
gives \(J_{\pi_{k}}\))
Step 3 (Policy Improvement) : Find a new policy \(\pi_{k+1}\) by
\(T_{\pi_{k+1}}J_{\pi_{k}} = TJ_{\pi_{k}}\)
\[\iff \pi_{k+1}(i) = argmin_{a\in A(i)} \sum_{j} P_{ij}(a)(g(i,a,j)) + \alpha J_{\pi_{k}}(j))\]
If \(J_{\pi_{k+1}}(i) < J_{\pi_{k}}(i)\) for at least one state \(i\), then
go to step 2 and repeat.
Remark:
Policy improvement claim holds even in the discounted setting.
Policy Improvement Claim:
Let \(\pi\) and \(\pi'\) be two proper policies such that
\[T_{\pi'}J_{\pi} = TJ_{\pi}\]
Then, \[J_{\pi'}(i) \leq J_{\pi}(i), \forall i\]
with strict inequality for at least one of the states if \(\pi\) is not
optimal.
Proof: Follows by a parallel argument to the proof in SSP case, and the details are omitted.
Policy Iteration example
Example 3.1 Consider the following set of states and actions
\(\mathcal{X}= \{1,2\}, \mathcal{A}= \{a,b\}\) \(P(a) = \begin{bmatrix} P_{11}(a) & P_{12}(a)\\ P_{21}(a) & P_{22}(a) \end{bmatrix}= \begin{bmatrix} 3/4 & 1/4\\ 3/4 & 1/4 \end{bmatrix}\)
\(P(b) = \begin{bmatrix} P_{11}(b) & P_{12}(b)\\ P_{21}(b) & P_{22}(b) \end{bmatrix}= \begin{bmatrix} 1/4 & 3/4\\ 1/4 & 3/4 \end{bmatrix}\) Costs: \(g(1,a)=2, g(1.b)=0.5\) \(g(2,a)=1, g(2,b)=3\)
discount: \(\alpha=0.9\)
Initialisation: \(\pi_0(1)=a, \pi_0(2)=b\)
Policy evaluation: Finding \(J_{\pi_0}\)
\(J_{\pi_0}(1)= g(1,a) + \alpha P_{11}(a) J_{\pi_0}(1) + \alpha P_{12}(a) J_{\pi_0}(2)\)
\(J_{\pi_0}(1)= g(2,a) + \alpha P_{21}(b) J_{\pi_0}(1) + \alpha P_{22}(b) J_{\pi_0}(2)\)
using MDP data, we have
\(J_{\pi_0}(1)= 2 + 0.9*{3/4}*J_{\pi_0}(1) + 0.9*{1/4}*J_{\pi_0}(2)\)
\(J_{\pi_0}(2)= 3 + 0.9*{1/4}*J_{\pi_0}(1) + 0.9*{3/4}*J_{\pi_0}(2)\)
solving
\(J_{\pi_0}(1)=24.12, J_{\pi_0}(2)=25.96\)
Policy improvement:
\(T_{\pi_1}J_{\pi_0}=TJ_{\pi_0}\)
\((TJ_{\pi_0})(1)=min\{2 + 0.9 (\frac{3}{4}*24.12 + \frac{1}{4}*25.96), 0.5 + 0.9 (\frac{1}{4}*24.12 + \frac{3}{4}*25.96)\}\)
\(=min\{24.5, 23.45\}= 23.45 (for action b)\)
\((TJ_{\pi_0})(2)=min\{1 + 0.9 (\frac{3}{4}*24.12 + \frac{1}{4}*25.96), 3 + 0.9 (\frac{1}{4}*24.12 + \frac{3}{4}*25.96)\}\)
\(=min\{23.12, 23.95\}= 23.12 (for action a)\)
\(\pi_1(1) = b, \pi_1(2) = a\)
Policy evaluation:
\(J_{\pi_1}(1) = 7.33, J_{\pi_1}(2) = 7.67\)
Policy improvement:
\(T_{\pi_2}J_{\pi_1}=TJ_{\pi_1}\)
\(\pi_1(1) = b, \pi_1(2) = a\)
so, stop and output \(\pi_2\)
3.8 Exercises
Exercise 3.2 Let \(f:\mathbb{R}^n \rightarrow \mathbb{R}^n\) be a contraction mapping with modulus \(\alpha\). We know that there exists an \(x^*\) such that \(f(x^*)=x^*\). Show that \[\left\| x^* - x\right\| \le \frac{1}{1-\alpha} \left\| f(x) - x\right\|.\]
In addition, if \(f\) is monotone, then prove that \[x \le y + \delta e \Rightarrow f(x) \le f(y) + \alpha |\delta|e,\] where \(\delta\) is a scalar, and \(e\) is the \(n\)-vector of ones.
Exercise 3.3 An energetic salesman works every day of the week. He can work in only one of two towns A and B on each day. For each day he works in town A (or B) his expected reward is \(r_A\) (or \(r_B\),respectively). The cost for changing towns is \(c\). Assume that \(c>r_A>r_B\) and that there is a discount factor \(\alpha<1\).
Answer the following:
Show that for \(\alpha\) sufficiently small, the optimal policy is to stay in the town he starts in, and that for \(\alpha\) sufficiently close to \(1\), the optimal policy is to move to town A (if not starting there) and stay in A for all subsequent times.
Solve the problem for \(c=3,r_A=2,r_B=1\), and \(\alpha=0.9\) using policy iteration.
Exercise 3.4 Consider an \(n\)-state discounted problem with bounded single stage cost \(g(i,a)\), discount factor \(\alpha \in (0,1)\), and transition probabilities \(p_{ij}(a)\). For each \(j=1,\ldots,n\), let \[m_j = \min_{i=1,\ldots,n}\min_{a\in A(i)} p_{ij}(a).\] For all \(i,j,a\), let \[\tilde p_{ij}(a) = \dfrac{p_{ij}(a) - m_j}{1- \sum_{k=1}^n m_k},\] assuming \(\sum_{k=1}^n m_k < 1\).
Answer the following:
Show that \(\tilde p_{ij}\) are transition probabilities.
Consider a modified discounted cost problem with single stage cost \(g(i,a)\), discount factor \(\alpha\left(1- \sum_{j=1}^n m_j\right)\), and transition probabilities \(\tilde p_{ij}(a)\). Show that this problem has the same optimal policy as the original, and that its optimal cost \(\tilde J\) satisfies \[J^* = \tilde J + \dfrac{\alpha\sum_{j=1}^n m_j \tilde J(j)}{1-\alpha} e,\] where \(J^*\) is the optimal cost vector of the original problem, and \(e\) is a \(n\)-vector of ones.
Exercise 3.5 Consider a discounted cost MDP with two states, denoted \(1\) and \(2\). In each state, there are two feasible actions, say \(a\) and \(b\). The transition probabilities are given by \[\begin{align} p_{11}(a)=p_{12}(a)=0.5;\quad p_{11}(b)=0.8, p_{12}(b)=0.2;\\ p_{21}(a)=0.4,p_{22}(a)=0.6;\quad p_{21}(b)=0.7, p_{22}(b)=0.3. \end{align}\] The single-stage costs are as follows: \[\begin{align} g(1,a,1)=-9, g(1,a,2)=-3; \quad g(1,b,1)=-4, g(1,b,2)=-4;\\ g(2,a,1)=-3, g(2,a,2)=7;\quad g(2,b,1)=-1, g(2,b,2)=19. \end{align}\] Assume that the discount factor \(\alpha\) is set to \(0.9\) and answer the following:
Find the optimal policy for this problem.
Start with a policy that chooses action \(a\) in each state, and perform policy iteration.
Start with the zero vector, and perform value iteration for four steps. Show the cost vector and the corresponding policy in each step.
Does the optimal policy change, when the discount factor is \(0.1\)? Justify your answer.
Exercise 3.6 Let \(f:\mathbb{R}^n \rightarrow \mathbb{R}^n\) be a contraction mapping with modulus \(\alpha\). We know that there exists an \(x^*\) such that \(f(x^*)=x^*\). Show that \[\left\| x^* - f^n(x)\right\| \le \frac{\alpha^n}{1-\alpha} \left\| f(x) - x\right\|,\quad \forall x \in \mathbb{R}^n, n\ge 1.\]
Exercise 3.7 Let \(f:\mathbb{R}^n \rightarrow \mathbb{R}^n\) be a contraction mapping w.r.t. the sup-norm. Let \(\alpha\) be the modulus, and \(x^*\) the fixed point of \(f\). Suppose \(f\) satisfies \[f(x+c e) = f(x) + \alpha c e, \textrm{ for all }x\in \mathbb{R}^n \textrm{ and scalar }c.\] In the above, \(e\) denotes the \(n\)-vector of ones. Assume that there exists a \(x' \in \mathbb{R}^n\), and scalar \(b\) such that \(f(x')-x' \le b\cdot e\).
Show that \[x^* \le f(x') + \frac{\alpha}{1-\alpha} b\cdot e \le x' + \frac{1}{1-\alpha} b\cdot e.\]
Exercise 3.8 Consider a discounted cost MDP with two states, denoted \(1\) and \(2\). In state \(1\), there are two feasible actions, say \(a\) and \(b\), while in state \(2\), there is only one action available, say \(c\). The transition probabilities are given by \[\begin{align} &p_{11}(a)=p_{12}(a)=0.5;\quad p_{11}(b)=0, \ p_{12}(b)=1;\\ &p_{21}(c)=0,\ p_{22}(c)=1; \end{align}\] The single-stage costs are as follows: \[\begin{align} g(1,a)=-5,\ g(1,b)=-10; \quad g(2,c)=1. \end{align}\] Answer the following:
Use the Bellman equation to calculate the optimal policy, when the discount factor \(\alpha\) is set to \(0.1\), \(0.5\) and \(0.9\).
Start with a policy that chooses action \(b\) in state \(1\), and perform policy iteration with \(\alpha=0.95\). Does the algorithm converge in two steps? Show your calculations for each policy iteration step.
Exercise 3.9 A manufacturer at each time period receives an order for her product with probability \(p\), and receives no order with probability \(1-p\). At any period, she has a choice of processing all the pending orders in a batch, or process no order at all. The cost per pending order in any period is \(c>0\), and the setup cost to process the pending orders is \(K>0\). She aims to find an optimal processing policy that minimizes, in expectation, the infinite horizon discounted cumulative cost, with a discount factor \(\alpha \in (0, 1)\). The setting has a constraint that the maximum number of orders that can be pending is \(n\).
Answer the following:
Letting the number of pending orders as the state, write down the Bellman equation for this problem.
Let \(J^*\) denote the optimal cost vector. Show that \(J^*(i)\) is monotonically non-decreasing in \(i\). Using this fact, show that a threshold-based policy is optimal.
Show that if policy iteration algorithm is initialized with a threshold policy, every subsequently generated policy will be a threshold policy.
Exercise 3.10 Consider a machine replacement problem over \(N\) stages. In each stage, the machine can be in one of the \(n\) states, denoted \(\{1,\ldots,n\}\). Let \(g(i)\) denote the cost of operating the machine in state \(i\) in any stage, with \[g(1) \le g(2) \ldots \le g(n).\] The system is stochastic, with \(p_{ij}\) denoting the probability that the machine goes from state \(i\) to \(j\). Note that the machine can either go worse or stay in the same conditions, which implies \(p_{ij} =0\) for \(j<i\). The state of the machine at the beginning of each stage is known and the possible actions are (i) perform no maintenance, i.e., let the machine run in the current state; and (ii) repair the machine at a cost \(R\). On repair, the machine transitions to state \(1\) and remains there for one stage.
Consider this problem in the discounted MDP framework, with a discount factor \(\beta \in (0,1)\). Assume \(p_{ij}=0\) if \(j<i\), and \(p_{ij} \le p_{(i+1)j}\) if \(i<j\). A threshold policy is defined to be a stationary policy that repairs if and only the state is equal to or greater than some state, say \(k\). Suppose we run policy iteration on this problem. If the initial policy is a threshold policy, show that all subsequent policies are threshold policies.
Exercise 3.11 Suppose \(f:\mathbb{R}^n \rightarrow \mathbb{R}^n\) satisfies \(\left\| f(x) - f(y)\right\| \le \left\| x - y\right\|\), where \(\left\| \cdot \right\|\) is the Euclidean norm. For some \(m\), \(f^m\) is a contraction mapping with modulus \(\alpha\), and fixed point \(x^*\). Here \(f^m(x)\) is \(f\) applied \(m\) times on \(x\).
Show that
\(x^*\) is the unique fixed point of \(f\).
\(\left\| x^*-x \right\| \le \frac{m}{(1-\alpha)}\left\| f(x)-x\right\|\), \(\forall x\in \mathbb{R}^n\).